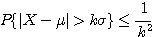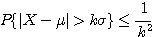Climatological Probabilities

A new feature has been added to the standardized anomaly maps. The color filled regions on the maps are the maximum climatological probability of the forecast meteorological parameter reaching the predicted standardized anomaly. This is based solely on the 60 year climate data set. This is not a probabilistic forecast, nor is it a tool to derive a "one in x number of year" event.

The climatological probabilities are derived using the Chebyshev Inequality. This is a probability theorem which states that in any data sample or probability distribution, nearly all the values are close to the mean value and provides a quantitative description of "nearly all" and "close to".

                                                                                      

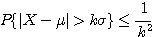
σ = standard deviation
k = standardized anomaly
μ = mean
X = random variable (height, temperature or other meteorological parameter)

In other words,  no more than 1/k² of the values are more than k standard deviations ( k is the value of the standardized anomaly) away from μ (the mean).

Example:

If the GFS suggests a 120 hour forecast of 500 hPa Heights at -6.0 standard deviations, we can compute this climatological probability using a "poor man's" PDF. This is done by taking 1 over the anomaly value, squaring it, multiplying the squared value by 2 (to account for both sides of the median), than converting to a percent. So 1/6² = 1/36, 2*36 =72, and 1/72 = 0.0138 or ~1.4% (see color bar on graphic).

In other words, the probability that the 500 hPa heights will differ from the climatological mean by more than 6 standard deviations is <= to 1.4%. Likewise the probability that the 500 hPa height will lie within 6 standard deviations of the mean is >= 98.6% . Please be mindful that we are using model forecast data and the various problems and biases of each model.

Since meteorological data does not typical fall in line with a Gaussian distribution, the ideal frame of reference for the standardized anomalies is a PDF for a given meteorological parameter on the grid. But since we can not easily compute a PDF for all of the points we forecast for, we opt for computing these climatological probabilities using this method. This accounts for the climatological variance and  provides a more reasonable climatological probability than extracting sigma values from a standard Bell Curve.