|
Propagation and movement
Propagation is influenced by a number of factors. One of the most important of these factors is where low level moisture convergence and instability is located relative to the initial convection or convective system. New cells form where there is moisture, instability and lift. The cold pool and resulting outflow boundary from the convection associated with the MCS plays and important role in determining where the low level convergence and instability will be located.
The system-relative inflow into the MCS also helps in determining the region of strongest moisture convergence and ascent. Finally, non-hydrostatic pressure gradients and buoyancy gradients may play aid in generating the rear inflow jet which in turn plays a role where the strongest low-level convergence is located relative to the system.
The following paragraphs will attempt to provide insight into how to operationally forecast the approximate direction and speed of propagation that will be associated with an MCS, and how the resulting propagation can be used to help forecast the movement of the MCS. System movement depends on cell movement and propagation. Individual cells usually move at around 90% of the mean wind with a slight deviation to the right. Finally, propagation is affected by what flank of the storm the new cells are forming on and by the rate of development of the new cells.
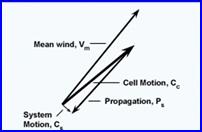
Chappell (1986) has noted that it is convenient to represent the movement of a convective system as the sum of the vector representing the movement wind flow and another vector representing the effects of propogation. |
|
Fankhauser (1964) noted that the movement of individual convective cells could be approximated by the mean wind of the cloud bearing layer. More recently, Corfidi et al (1996) suggested that during MCS initiation the movement of the convective cells can be approximated by the mean wind between 850- and 300-hPa as defined by,
Vcell=(V850+V700+V500+V300)/4
Corfidi et al. created two scatter diagrams showing that there is a high correlation between the 850-300 hPa mean wind speed and direction at the time of convective initiation. |
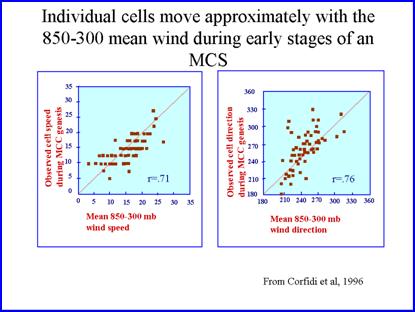
|
However, it is important to note that for convection with unusually low cloud tops using the 850-300 hPa mean wind may be a poor approximation for cell motion since the cloud layer may be considerably lower, and the clouds move with the winds within the cloud bearing layer. In addition, for potentially deeper clouds (equilibrium levels higher than 300-hPa), you may need to use 850-200 hPa layer for mean wind calculations to represent the movement of individual cells.
When you are trying to predict the motion of individual cells, remember to try to anticipate whether you will be dealing with low topped convection or not. The equilibrium level provides the top limit to the cloud bearing layer while the LCL can be used to estimate the bottom of the cloud bearing layer. The next step is to find a way to approximate the propagation vector. The scatter diagram shows that the direction of propagation is anti-parallel (in the opposite direction) to the low level jet (see figure). However, there were two significant outliers. The big question then becomes how to determine the magnitude of the vector. Corfidi et al. (1996, henceforth called (CMF) reasoned that the stronger the low level jet, the stronger low level convergence should be along the flank of the MCS that is being impinged upon by the jet. They therefore assumed that the propagation vector was equal to and of opposite sign as the low level jet. Therefore, Vprop= -Vllj |
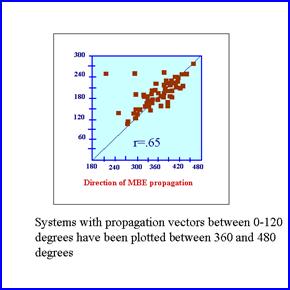
|
They then tested the following formula to see whether it provided a good estimate of the motion of the most active elements of the convection system.
VMCS=Vcell-Vllj
Where VMCS stands for MCS motion, Vcell stands for motion of the individual cells which is approximated by the mean wind between 300 hPa and 850 hPa, and Vllj is the vector describing the low level jet.
|
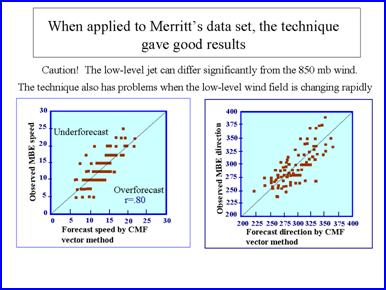
|
More recently, Corfidi (2003) has noted that the wind profiles associated with quasi-stationary convective systems was sometimes very similar to the vertical wind profile found for the Trailing Stratiform (Parker and Johnson TS type) MCSs (derechoes) studied by Johns and Hurt (1987). Therefore, the original CMF method underestimated the speed of movement for a number of these forward propagating MCSs. The original technique does not work as well when: 1) there is moist unstable air downstream from where the initial thunderstorms develop or are expected to develop, 2) when the mid level flow is relatively strong, 3) when there is a dry layer at mid levels.
Corfidi (2003) has suggested that the original vector technique would sometimes seriously under-estimate the motion of a squall line because it failed to account for propagation that occurs in the down-shear or downwind direction. A forecaster needs to consider the direction of greatest system-relative convergence and the distribution of surface-based instability when applying the vector technique. The latter is often determined by the evolution of the cold pool and associated outflow boundary or gust front. Corfidi offers a hypothetical example of the evolution of a gust front associated with a fairly uniform vertical wind profile (see figure below). In such a case the leading edge of the gust front will move with the mean wind speed. |
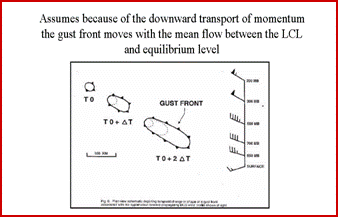
|
is a good bet when the mid-level wind field is relatively strong, especially if there is a dry layer to promote the downward transfer of momentum. The resulting motion of the MCS is the sum of the mean wind and a system-relative propagation vector which is dependent on the mean wind and the low-level jet. For example, if the convection is moving east at 40 kts, the system is experiencing inflow of similar magnitude assuming there is no low level wind. Relative to the west-to-east moving convective system, easterly winds are feeding into it. If the airmass is moist and unstable on the east side of the system, then the system relative inflow will produce moisture convergence and convection along the leading edge of the convection.
The inflow due to the system motion acts the same way that the low-level jet worked in the original CMF vector method. System movement imparts a system-relative inflow of equal magnitude to the system movement but in the opposite direction. To a west-to-east moving system, this is analogous to having an east wind on the east side of the system. Remember in the original CMF vector method, the propagation vector was equal in magnitude but opposite in direction to the low level jet. In the revised technique, the system-relative low-level wind acts similarly. Therefore, the MCS movement vector from the original MCF method is added to the vector that describes the mean wind. Essentially, in the revised vector method you double the mean wind and then subtract the low level jet from that sum.
VMCS=2(Vcell)-Vllj
When using the vector method it is important to remember that the decision on whether to use the original CMF method or the revised method should be dependent on the type of MCS that is anticipated. Most of the time the original vector method should work best for back-building convective system or for systems in which the propagation due to new cells forming on the rearward flank acts to slow system movement. |
|
Along the leading edge of the gust front, a forward propagating convective system is typically found. However, farther west along the gust front, outflow boundary may become aligned parallel to the mean flow allowing training of cells. Essentially, the vector method says that if the air mass is unstable downstream of the initial convection, then a forward propagating MCS |
|
The Revised Corfidi Vector method |
|
Original Corfidi vector method |